¿QUE ES EL SISTEMA DE COORDENADAS Y PARA QUE SIRVEN?

Un arreglo de dos rectas numéricas (una en posición horizontal y otra en posición vertical) unidas en sus ceros (origen) se denomina sistema de coordenadas rectangulares o plano cartesiano, en honor a René Descartes.

La recta horizontal se llama eje X y la recta vertical, eje Y. Observa que el sistema de coordenadas divide al plano en cuatro regiones, llamadas cuadrantes.

El primer cuadrante tiene la parte positiva del eje X y del eje Y.

El segundo cuadrante tiene la parte negativa del eje X y la parte positiva del eje Y.

El tercer cuadrante tiene la parte positiva del eje X y la parte negativa del eje Y.

El cuarto cuadrante tiene la parte negativa del eje X y la parte negativa del eje Y.

Note que la lista de coordenadas puede expresar tanto la posición de un punto como las componentes de un vector en notación matricial.

La distancia entre dos puntos cualesquiera vendrá dada por la expresión:

d_{\overline {AB}}={\sqrt {(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}}\,

Esto es, distancia P₁ P = 3 –1 =2 , distancia P P₂ = -1 – (-3) =2

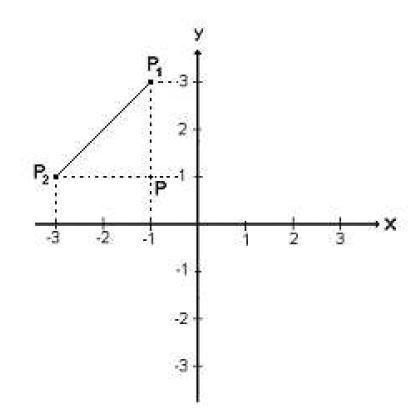
Por lo tanto, aplicando el teorema de Pitágoras, la distancia P₁ P₂ está dada por:

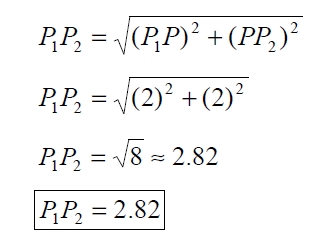
Entrena tu mente

a continuación resuelve los siguientes problemas planteados

1.-En el sistema de coordenadas rectangulares ubica las siguientes coordenadas y obtén su perímetro de la figura formada

A(5,5) B(-5,5) C(-5,-5) D(5,-5) REALIZA TU GRÁFICA

2.-A partir de las siguientes coordenadas obtén el área de la figura proporcionada

A(4,-8) B(-4,-8) C(-4,8) D(4,8) REALIZA TU GRÁFICA

°SEGMENTOS RECTILÍNEOS

Estos segmentos se dividen en dos los dirigidos y los no dirigidos. los dirigidos son la porción de la recta comprendida entre los puntos A y B, en donde los dos puntos se les conoce como extremos. en geometría analítica, al punto A se le conoce como origen o punto inicial y al punto B como el punto final. por lo tanto el segmento AB ademas de tener la magnitud, esta dirigido o tiene sentido desde A hasta B y debe de indicar con una flecha. Con esto podemos concluir que el segmento BA tiene dirección o sentido contrario a AB es decir AB=-BA

segmento rectilíneo NO dirigido.Un segmento no dirigido es aquel al que no se le considera un sentido; por lo tanto, se puede expresar en cualquier orden, es decir, siempre se le considera como positivo, cualquiera que sea su sentido. Entonces, para escribir dicho segmento utilizamos la notación del valor numérico o valor absoluto. Por lo tanto tenemos que decir AB=BA

distancia entre dos puntos

El Plano cartesiano se usa como un sistema de referencia para localizar puntos en un plano.

Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.

Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 – x1).

Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas. (y1 - y2)

Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación

esta es la formula que se utiliza para calcilar la distancia entre el segmento AB

Calcula la distancia entre los puntos P 1 (7, 5) y P 2 (4, 1)

ejercita tu mente: a continuación realiza las actividades que se te piden

1.- calcula la distancia entre los puntos A(-5,7) B(5,7)

2.-calcula la distancia entre los puntos P(9,8) Y Q(-5,-7)

DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA

Durante nuestro estudio de la Geometría Analítica, nos vamos a encontrar con un método interesante para poder calcular las coordenadas de un punto P (o sea un punto cualquiera que llamamos “P”), que está dividido por un segmento cuyas extremidades son el P1 (x1, y1) y P2 (x2, y2) en la razón dada por la siguiente relación:

$\displaystyle r=\frac{{{P}_{1}}P}{P{{P}_{2}}}$

Hasta este punto puede ser confuso lo explicado, pero no es necesario enredarse con la definición. Mas abajo veremos la definición en una gráfica y nos daremos una mejor idea de lo que intentamos explicar, y ver como llevar a cabo el procedimiento para encontrar la fórmula de la división de un segmento en una razón dada , y poder resolver ejercicios sin dificultad alguna. Es necesario que para estudiar este tema se tenga idea de como despejar variables y conocimiento de álgebra.

$\displaystyle x=\frac{{{x}_{1}}+r{{x}_{2}}}{r+1}$

1.- Hallar las coordenadas del punto P que divide al segmento determinado por A (5, 3) y B (-2,8) en la razón r = 3/4

Solución:

Sin tanta complicación, podemos utilizar nuestras fórmulas y sustituir nuestros datos.

Recordar que en el punto A, tenemos lo siguiente:

$\displaystyle {{x}_{1}}=5$

$\displaystyle {{y}_{1}}=3$

Y para el punto B

$\displaystyle {{x}_{2}}=-2$

$\displaystyle {{y}_{2}}=8$

Ahora, sustituyendo tenemos:

$\displaystyle x=\frac{{{x}_{1}}+r{{x}_{2}}}{r+1}=\frac{5+\left( \frac{3}{4} \right)\left( -2 \right)}{\frac{3}{4}+1}=\frac{5-\frac{6}{4}}{\frac{7}{4}}=\frac{\frac{14}{4}}{\frac{7}{4}}=\frac{14(4)}{7(4)}=\frac{14}{7}=2$

$\displaystyle x=2$

Concluimos que x = 2, ahora hagamos lo mismo para “y”.

$\displaystyle y=\frac{{{y}_{1}}+r{{y}_{2}}}{r+1}=\frac{3+\left( \frac{3}{4} \right)(8)}{\frac{3}{4}+1}=\frac{3+\frac{24}{4}}{\frac{7}{4}}=\frac{3+6}{\frac{7}{4}}=\frac{9}{\frac{7}{4}}=\frac{36}{7}\approx 5.143$

$\displaystyle y\approx 5.143$

El valor de “y” será un valor aproximadamente de 5.143.

De forma gráfica esto es.

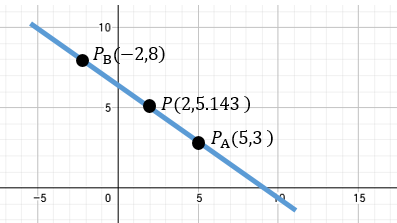
EJERCITA TU MENTE

Hallar las coordenadas del punto P (x,y) que divide al segmento determinado por A (-2, 5) y B (10,-2) en la razón r = 2/3

Los extremos del diámetro de una circunferencia son A (3, -2) y B (5,6), encuentra las coordenadas del centro

Perímetro y Área de Polígonos en plano cartesiano

Resultado de imagen para Determinación del perímetro de un polígono en el plano cartesiano

En este tema PERÍMETROS Y ÁREAS, analizamos como obtener el perímetro y

la área de un polígono de n lados que esta graficado en un plano cartesiano y

en donde solo sabemos sus coordenadas, para ello es necesario retomar una

breve definición de PERÍMETRO Y ÁREA, en cuanto a geometría analítica:

El perímetro y el área son magnitudes fundamentales en la determinación

de un polígono o una figura geométrica; se utiliza para calcular la frontera

de un objeto, tal como una valla. El área se utiliza cuando queremos obtener

la superficie interior de un perímetro que se desea cubrir con algo, tal como

césped o fertilizantes.

El área es una medida de la extensión de una superficie, expresada en

unidades de medida denominadas superficiales. Para superficies planas

el concepto es más intuitivo. Cualquier superficie plana de lados rectos

puede triangularsey se puede calcular su área como suma de las áreas

de dichos triángulos. Ocasionalmente se usa el término "área" como

sinónimo de superficie, cuando no existe confusión entre el concepto

geométrico en sí mismo (superficie) y la magnitud métrica asociada al

concepto geométrico (área).

Ahora el siguiente paso es: ¿Cómo obtener el périmetro de un poligono

de n lados en un plano cartesiano?

Para conocer el perímetro de un polígono cualquiera debemos medir

y sumar las longitudes de sus lados. Algunas figuras, debido a que tienen l

ados iguales, tienen fórmulas fáciles y rápidas con las que podemos calcular

su perímetro

LA RECTA COMO LUGAR GEOMETRICO.

Un lugar geométrico es un conjunto de puntos que satisfacen determinadas propiedades geométricas. Cualquier figura geométrica se puede definir como el lugar geométrico de los puntos que cumplen ciertas propiedades si todos los puntos de dicha figura cumplen esas propiedades y todo punto que las cumple pertenece a la figura.
Es un conjunto de puntos formados por el producto entre dos conjuntos tales que un subconjuntos de ellos satisfacen una propiedad y que solo estos puntos satisfacen dicha propiedad.
Estos son varios ejemplos de lugares geométricos en el plano:

El lugar geométrico de los $P$ que equidistan a dos puntos fijos $A$ y $B$ (los dos extremos de un segmento de recta, por ejemplo) es una recta, llamada mediatriz. Dicho de otra forma, la mediatriz es la recta que interseca perpendicularmente a un segmento $A B$ en su punto medio ( $(A + B) / 2$ ).

La bisectriz es también un lugar geométrico. Fijado un ángulo, delimitado por dos rectas, la bisectriz es la recta que, pasando por el vértice (punto donde se cortan dichas rectas), lo divide por la mitad. Esta recta cumple la propiedad de equidistar a las dos anteriores, convirtiéndose la bisectriz en un caso particular del lugar geométrico que sigue a continuación.

Generalizando la propiedad de equidistancia a dos rectas, obtenemos que la paralela media es el lugar geométrico de los puntos que las equidistan. Se observa que, bajo el punto de vista de que las rectas paralelas se cortan en el infinito -se elimina, pues, la noción de paralelismo-, pasa a ser un sinónimo de la bisectriz, donde el ángulo ha tomado valor nulo. Si, por el contrario, se diferencia el concepto de paralelismo, la bisectriz vuelve a ser, como se ha dicho antes, un caso particular de esta definición y el caso de rectas paralelas, con ángulo 0, es disjunto al de las bisectrices (ángulo no nulo).

Las secciones cónicas pueden ser descritas mediante sus lugares geométricos:

Una circunferencia es el lugar geométrico de los puntos cuya distancia a un punto determinado, el centro, es un valor dado (el radio).

Una elipse es el lugar geométrico de los puntos tales que la suma de su distancia a dos puntos fijos, los focos, es una constante dada (equivalente a la longitud del semieje mayor de la elipse).

La parábola es el lugar geométrico de los puntos cuya distancia a un foco equivale a su distancia a una recta llamada directriz.

La hipérbola es el lugar geométrico de los puntos tales que el valor absoluto de la diferencia entre sus distancias a dos puntos fijos, los focos, es igual a una constante (positiva), que equivale a la distancia entre los vértices.

Figuras muy complejas pueden ser descritas mediante el lugar geométrico generado por los ceros de una función o de un polinomio. Por ejemplo, las cuádricas están definidas como el lugar geométrico de los ceros de polinomios cuadráticos. En general, los lugares geométricos generados por los ceros del conjunto de polinomios reciben el nombre de variedad algebraica, las propiedades de dichas variedades se estudian en la geometría algebraica. q ue es radio es un circulo grande q nos sirve para poder calcular las medidas de un circulo

Ángulo de inclinación.

Dada una recta l que no sea paralela al eje X y que toque a este en uno de sus puntos, es posible determinar un ángulo, que se obtiene al girar una semirecta, que inicialmente se ubica sobre el eje X, en sentido contrario a las manecillas de reloj, hasta tocar a la recta l.

Al ángulo así obtenido se le llama ángulo de inclinación de la recta l.

Pendiente de una recta.

Se denomina pendiente o coeficiente angular de una recta a la tangente de su ángulo de inclinación. Se utiliza la letra m para denotar a la pendiente de una recta y se expresa por m = tan Θ.

A la pendiente de una recta también se le conoce como tasa de cambio o razón de cambioporque indica cuánto crece o decrece una recta.

Si la curva que dibujamos en un plano es una línea recta, su tasa de crecimiento permanece constante, sin importar en qué puntos de la recta sea medida.

Criterios.

El ángulo de inclinación puede asumir cualquier valor entre 0° y 180° (0° ≤ Θ ≤ 180°), por lo que el signo de la pendiente puede determinarse como sigue:

(a) m es positiva si 0° < Θ < 90°.

(b) m es negativa si 90° < Θ ≤ 180°.

(d) m = ∞ (es indefinida) si Θ = 90°.