Concepto de parábola y sus elementos
Una parábola queda definida por el conjunto de los puntos del plano que equidistan de una recta fija y un punto fijo:
Elementos de la parábola

Foco: Es el punto fijo F.
Directriz: Es la recta fija D.
Parámetro: A la distancia entre el foco y la directriz de una parábola se le llama parámetro p.
Eje: La recta perpendicular a la directriz y que pasa por el foco recibe el nombre de eje. Es el eje de simetría de la parábola.
Vértice: Es el punto medio entre el foco y la directriz. También se puede ver como el punto de intersección del eje con la parábola.
Radio vector: Es el segmento que une un punto cualquiera de la parábola con el foco.
Elementos de la parábola

Foco: Es el punto fijo F.
Directriz: Es la recta fija D.
Parámetro: A la distancia entre el foco y la directriz de una parábola se le llama parámetro p.
Eje: La recta perpendicular a la directriz y que pasa por el foco recibe el nombre de eje. Es el eje de simetría de la parábola.
Vértice: Es el punto medio entre el foco y la directriz. También se puede ver como el punto de intersección del eje con la parábola.
Radio vector: Es el segmento que une un punto cualquiera de la parábola con el foco.
upongamos que el vértice de una parábola cuando su eje focal es paralelo al eje Y se halla situado en el punto (h,k).
En este caso tendremos que trasladar el vértice al nuevo punto quedándonos establecida la fórmula:
Hacemos operaciones:
Damos valores a:
Sustituyendo estos valores en (I) obtenemos la ecuación general de la parábola:
Cuando su eje focal es paralelo al eje X se halla situado en el punto (h, k) la fórmula es:
26.42 Una parábola tiene su foco en el punto F(5,0) y su vértice en V(1,0). ¿Cuál es su ecuación? Dibuja la parábola.
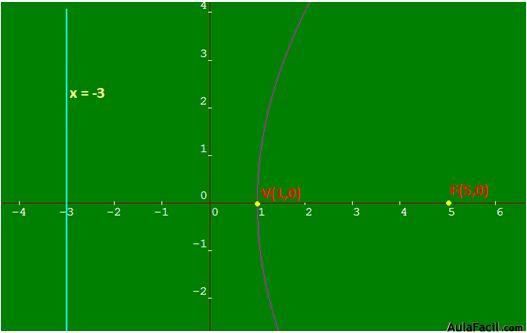
Solución
El punto (h, k) corresponde a (1, 0)
La ecuación es:
EJERCITA TU MENTE
Concepto y elementos de la elipse
Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.

Elementos de la elipse:
1. Focos: Son los puntos fijos F y F'.
2. Eje focal: Es la recta que pasa por los focos.
3. Eje secundario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.
5. Radios vectores: Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'.
6. Distancia focal: Es el segmento segmento de longitud 2c, c es el valor de la semidistancia focal.
7. Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
8. Eje mayor: Es el segmento segmento de longitud 2a, a es el valor del semieje mayor.
9. Eje menor: Es el segmento segmento de longitud 2b, b es el valor del semieje menor.
10. Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor.
11. Centro de simetría: Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.
Relación entre la distancia focal y los semiejes

Demostración de la ecuación de la elipse (origen - horizontal)
Elipse centrada en el origen de coordenadas y eje mayor el eje “X”.
Caso I Elipse horizontal
Caso I Elipse horizontal

La ecuación ordinaria para una elipse horizontal, con eje simetría el eje “X” es
La figura muestra además la relación pitagórica entre a, b y c, es decir,
Ejemplo: Dada la ecuación de la elipse  determinar: centro, coordenadas de los vértices, eje mayor, eje menor, las coordenadas de los focos y hacer la gráfica.
determinar: centro, coordenadas de los vértices, eje mayor, eje menor, las coordenadas de los focos y hacer la gráfica.
Solución
1. Como los coeficientes de  es uno, entonces la elipse está centrada en el origen de coordenadas.
es uno, entonces la elipse está centrada en el origen de coordenadas.
C(0, 0)
Como a > b, entonces el eje mayor es el eje “X” por tanto

El valor de c se determina con la relación Pitagórica

Nota: c es un número positivo, ya que la distancia siempre es positiva.
Demostración de la ecuación de la elipse (origen - vertical)
Elipse centrada en el origen de coordenadas y eje mayor el eje “Y”.
Caso II Elipse vertical
Caso II Elipse vertical

El eje mayor está en el eje de las y. Las intercepciones en x son (±b, 0) y las intercepciones en y son (0, ±a).
El eje mayor está en el eje de las y.
Dese cuenta que el eje mayor es horizontal si el término
Hallar la ecuación de una grafica de elipse [centro=(0,0)]
Si el centro de la elipse C(x0, y0) y el eje principal es paralelo a OX, los focos tienen de coordenadas F(X0+c, y0) y F'(X0-c, y0). Y la ecuación de la elipse será:


Al quitar denominadores y desarrollar se obtiene, en general, una ecuación de la forma:

Donde A y B tienen el mismo signo.
Ecuación de eje vertical de la elipse
Si el centro de la elipse C(x0, y0) y el eje principal es paralelo a OY, los focos tienen de coordenadas F(X0, y+c) y F'(X0, y0-c). Y la ecuación de la elipse será:



Al quitar denominadores y desarrollar se obtiene, en general, una ecuación de la forma:
Donde A y B tienen el mismo signo.
Ecuación de eje vertical de la elipse
Si el centro de la elipse C(x0, y0) y el eje principal es paralelo a OY, los focos tienen de coordenadas F(X0, y+c) y F'(X0, y0-c). Y la ecuación de la elipse será:

Hallar los elementos de una grafica de elipse [centro=(0,0)]
Ejemplo:
Hallar los elementos característicos y la ecuación reducida de la elipse de focos: F'(-3, 0) y F(3, 0), y su eje mayor mide 10.

Semieje mayor

Semidistancia focal

Semieje menor

Ecuación reducida

Excentricidad

Hallar los elementos característicos y la ecuación reducida de la elipse de focos: F'(-3, 0) y F(3, 0), y su eje mayor mide 10.

Semieje mayor
Semidistancia focal
Semieje menor
Ecuación reducida
Excentricidad
Elementos de la elipse (origen) dada su ecuación
Ejemplo:
Dada la ecuación reducida de la elipse  , hallar las coordenadas de los vértices de los focos y la excentricidad.
, hallar las coordenadas de los vértices de los focos y la excentricidad.
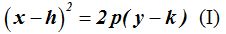
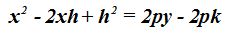
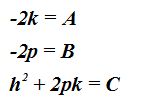
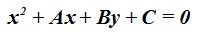
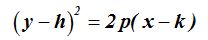
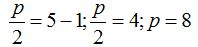
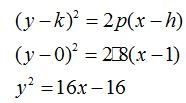
No hay comentarios:
Publicar un comentario